Med hjälp av derivata kan du ta reda på om en funktion växer eller avtar. Vi kan även avgöra om en punkt är en extrempunkt (minimipunkt eller maximipunkt) och om funktionsvärdet där är ett extremvärde.
Beakta funktionen f(x)=x^3-6x^2-15x .
Dess derivata är f´(x)=3x^2-12x-15 och nu söker vi då f´(x)=0 .
3x^2-12x-15 =0 \\
x^2-4x-5=0 \\
x=2 \pm \sqrt{9} \\
x_1=5 \\
x_2=-1
Därmed är derivatan noll i punkterna (5, f(5)) och (-1, f(-1)).
Minimipunkt eller maximipunkt
Typ av punkt kan bestämmas med hjälp av teckenschema eller andraderivata. Här visas hur andraderivata används.
f´´(x)=6x-12 \\
f´´(5)=28 \,(\text{Positiv andraderivata})\\
f´´(-1)=-18 \,(\text{Negativ andraderivata})I (5, f(5)) har vi därmed en minimipunkt och i (-1, f(-1)) har vi en maximipunkt. Ritas kurvan till funktionen ut ges följande.
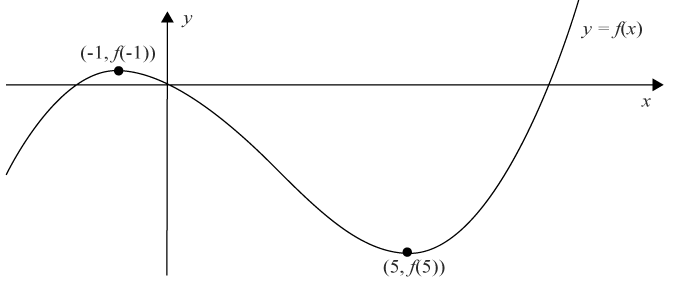
Lokala och globala värden
Låt säga att ovan nämnda funktion avgränsas i intervallet
-2\leq x \leq 9
Ritas funktionen ut ges då följande.
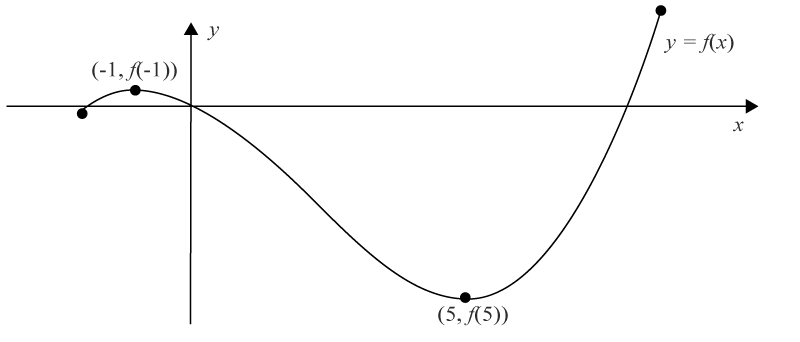
och (-1, f(-1)) är fortfarande extrempunkter men även intervallets ändpunkter är nu extrempunkter.
(-2, f(-2)) är en lokal minimipunkt.
(-1, f(-1)) är en lokal maximipunkt
(5, f(5)) är en lokal och global minimipunkt då det är intervallets minsta värde.
(9, f(9)) är en lokal och global maximipunkt då det är intervallets största värde.